数模自学笔记——数理统计 | 小灰灰灰灰的博客

面对一批数据进行分析和建模，首先需要掌握参数估计和假设检验这两个数理统计的最基本方法，给定的数据满足一定的分布要求后，才能建立回归分析和方差分析等数学模型。
——《数学建模算法与应用（第2版）》（司守奎主编）

“概率论与数理统计”，数理统计就是基于概率论的一个学科。只是数模对其要求会比概率论课程高一些。

# 参数估计和假设检验

推导见概率论课本。

# 正态分布

正态分布的 $\mu$ 的一个置信水平为 $1-\alpha$ 的置信区间为 $$\bigg( \overline{X} \pm \frac{S}{\sqrt{n}}t_{\alpha/2}(n-1) \bigg)$ $ MATLAB 也直接提供了 $t$ 检验的公式：

x0=[506  508  499  503  504  510  497  512
514  505  493  496  506  502  509  496];
x0=x0(:);
mu=mean(x0);
[h,p,ci]=ttest(x0,mu,0.05)

而正态分布的 $\sigma^2$ 的一个置信水平为 $1-\alpha$ 的置信区间为 $$\bigg( \frac{(n-1)S}{\chi^2_{1-\alpha/2}(n-1)}, \frac{(n-1)S}{\chi^2_{\alpha/2}(n-1)}\bigg)$ $ MATLAB 也直接提供了方差检验的公式：

x2=[6.661, 6.661, 6.667, 6.667, 6.664];
[h4,p4,ci4,st4]=vartest(x2,var(x1),'Alpha',0.1)

总体均值差的公式为 $$\bigg(\overline{X_1}-\overline{X_2} \pm t_{\alpha/2}(n_1+n_2-2)S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\bigg)$ $ 可使用 ttest2 进行检验。

x1=[6.683, 6.681, 6.676, 6.678, 6.679, 6.672];
x2=[6.661, 6.661, 6.667, 6.667, 6.664];
[h,p,ci,st]=ttest2(x1,x2,'Alpha',0.1)

# 经验分布函数

概率论没讲过。书上也讲了一堆定义，反正挺晦涩难懂的。又说这个函数收敛于什么什么函数，总之奇奇怪怪的。

一上图，我就猜到什么意思了。

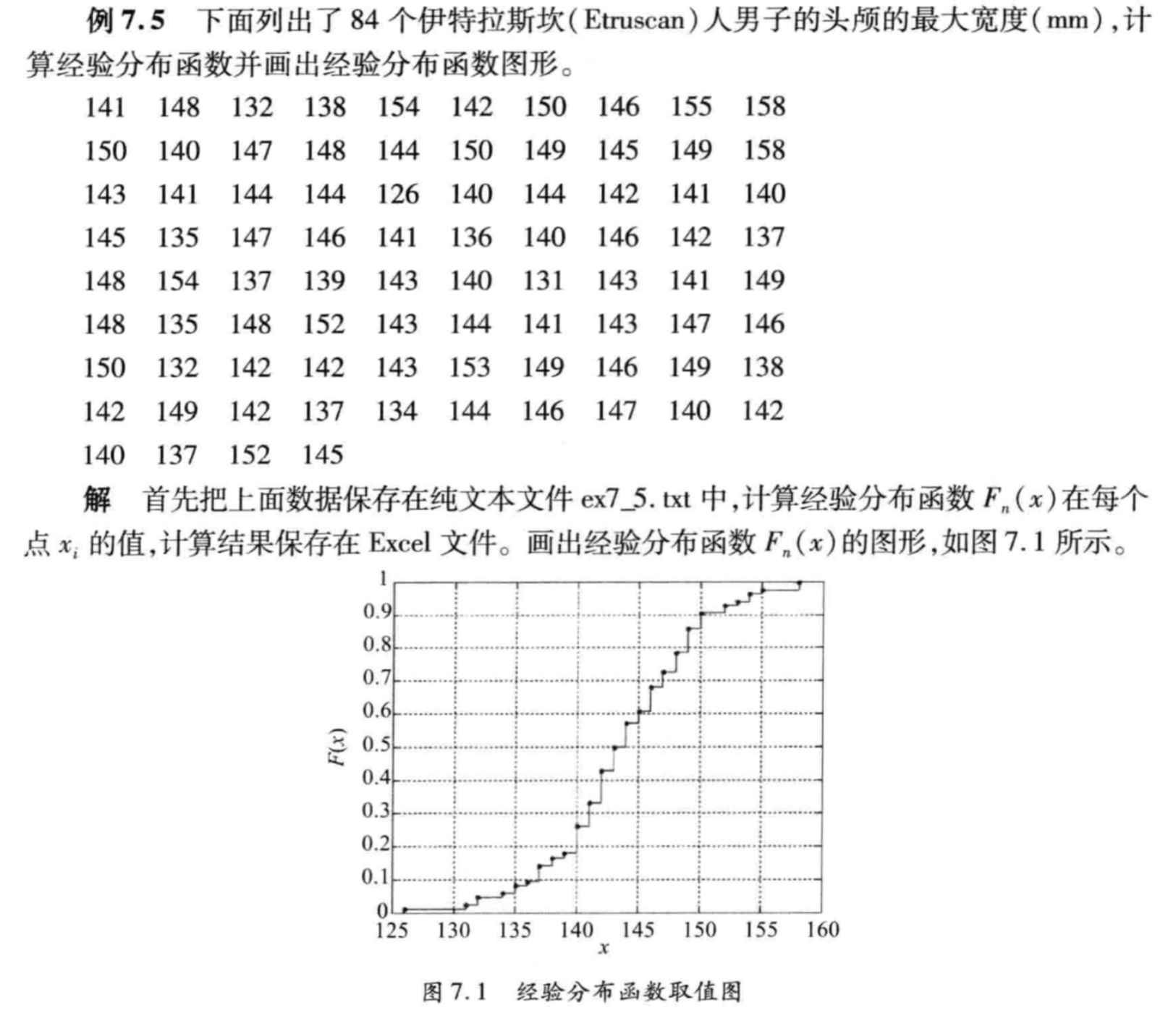
经验分布函数

可以猜到，上面画的这个图就是经验分布函数，颇有离散型随机变量分布函数的意味。

但是，当点足够多的时候，这个经验分布函数就趋近于真实的函数了！（那是不是跑一下插值就是连续函数，美滋滋了）

如果真的用到了，再去翻书的定义吧（P130）。

# Q-Q 图

qwq

Q：Quantile，分位数

Q-Q 图的作用是，给定一组观测数据（如上的经验分布函数的数据），然后确定了分布模型的参数 $\theta$ 后，直观地检测拟合效果好坏的方法。

其方法大致是：将这些观测数据确定的经验分布函数的分位数，和计算出的分布函数对应的分位数，分别作为横纵坐标，画在一张图上。如果拟合效果好，这些点应该在 $y=x$ 上。如下图：

Q-Q 图

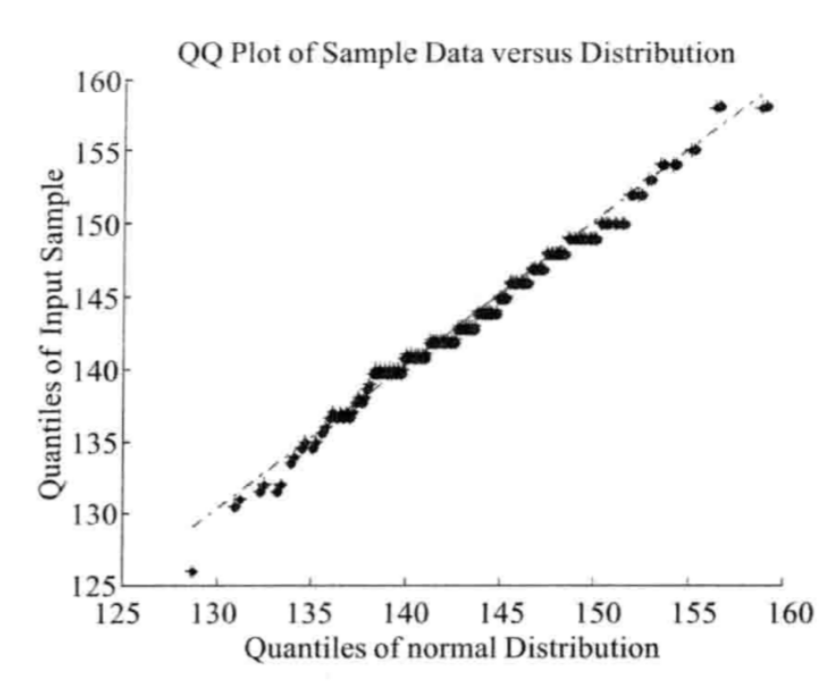
具体作法依旧是用到的时候翻书。

# 非参数检验

非参数检验，顾名思义，就是检验的不是参数，而是整个分布函数。

非参数检验又分为两种： $\chi^2$ 拟合优度（goodness-of-fit）检验和柯尔莫哥洛夫检验。

前者可检验离散性和连续型变量。方法大致是将 $(-\infty, +\infty)$ 分为 $k$ 段，计算每段的概率和观测频率，通过运算得到 $\chi^2$ 值用以检验。

柯尔莫哥洛夫检验。。。留个坑吧。这部分都挺难的，准备先粗略过一遍，所有章节学完以后，再回来看。

# 秩和检验

秩 Rank：排序后的名次

用于判断两个分布有无显著差异。

方法是，将两个分布的数混起来然后排序。排完序以后，将其中一个分布的名次数加起来，称作秩和。

然后根据 $n_1$ 、 $n_2$ 、 $t$ 查表。如果秩和在中间部分，则可认为无明显差异。

# Bootstrap

这个是统计学的 Bootstrap，不是网页 css 框架的那个。

Bootstrap 是在样本点不够的情况下，从已知的信息中（有放回地）抽抽抽。抽出来的数每 $n$ 个数分为一组，美其名曰，一组容量为 $n$ 的样本。

对于每一组样本都可以算出一个随机变量，就可以对算出来的所有随机变量进行计算，得到该随机变量的均方误差、标准误差、区间估计等信息。

这种方法的好处在上面也就提到了，在样本点较少的情况下会有奇效。

这种方法需要在计算机上做大量的计算，随着计算机威力的增长，它也成为了流行的方法。

# 非参数 Bootstrap

非参数 Bootstrap 是指，分布函数未知，仅知道一堆样本点。现在要计算某估计量 $\theta$ （这里估计量甚至可以取中位数）的标准差 $\sqrt{D(\hat\theta)}$ 、均方误差 $MSE=E[(M-\theta)^2]$ 和置信区间等。

那么就只需要在给出的样本点里面抽抽抽就可以了。

我们在给定的样本中有放回地抽 $B$ 个大小为 $n$ 的样本（共抽 $Bn$ 次），对于每个样本，计算出 $\theta$ 的估计 $\hat\theta^*_i$ ，则 $\theta$ 的标准误差的 Bootstrap 估计为

\hat\sigma_{\hat\theta}=\sqrt{\frac{1}{B-1}\sum_{i=1}^B(\hat\theta^*_i-\overline\theta^*)^2}

其中 $\overline\theta^*$ 是原样本的 $\theta$ 的估计值。

$\theta$ 的均方误差的 Bootstrap 估计为

E_*(\theta^*)=\frac{1}{B}\sum_{i=1}^B(\hat\theta^*_i-\overline\theta^*)^2

MATLAB 也提供了 bootstrp 函数，估计量函数可用匿名函数指定，函数返回 $B$ 个 $\hat\theta^*_i$ 。

Bootstrap 置信区间的求法相对有所不同。其方法是，对算出来的 $B$ 个 $\hat\theta^*_i$ 进行排序。在 $\alpha/2$ 和 $1-\alpha/2$ 位（下标为 $\left[B \times \alpha/2, B \times(1-\alpha/2) \right]$ ）的就是置信水平 $1-\alpha$ 的 Bootstrap 置信区间。

# 参数 Bootstrap

对于参数 Bootstrap，相较于上面多了一个分布函数的形式 $F(x;\beta)$ （参数未知）。

其做法是，先对分布函数和已知的样本点，计算出 $\beta$ 的最大似然估计 $\hat\beta$ ，并代入至函数得 $F(x;\hat\beta)$ 。

然后，用分布函数 $F(x;\hat\beta)$ 产生 $Bn$ 个随机点。接下来的操作就和上面完全一样了。

# 方差分析

方差分析用于检验单因素是否有影响，即在水平 $A_j (j=1,2,\cdots,s)$ 下，进行多次试验，验证需要假设 $\mu_1=\mu_2=\cdots=\mu_s$ 。

3 个前提：

总体服从正态分布
个体是相互独立
组间方差相等

具体验证方法依旧是看书。

# 回归分析

这部分的公式较多，所以依旧是只介绍思想，具体公式请范翻书。

# 拟合和回归

拟合和回归分析的区别在哪里呢？

In short, curve fitting is a set of techniques used to fit a curve to data points while regression is a method for statistical inference. Curve fitting encompasses methods used in regression, and regression is not necessarily fitting a curve.
Both curve fitting and regression try to find a relationship between variables. In the case of regression there are many more constraints in that relationship. What's the difference between curve fitting and regression | Quora (opens new window)

翻译一下就是拟合是一些算出曲线的方法，而回归分析还要进行分析。

# 多元线性回归

多元线性回归分析的模型是：

\begin{cases} y = \beta_0 + \beta_1x_1 + \cdots + \beta_mx_m + \varepsilon \\ \varepsilon \sim N(0, \sigma^2) \end{cases}

其中 $\beta_i$ 为未知系数，称为回归系数。

现在测得 $n$ 个独立的 $[y, x_1, x_2, \cdots, x_m]$ 的观测值，第 $i$ 个为 $[b_i, a_{i1}, a_{i2}, \cdots, a_{im}]$ 。

$m$ 个待估计参数、 $n$ 组观测值。

第一步，进行参数估计。即以最小二乘法的原理，按公式计算得 $m$ 个 $\beta$ ，以及残差（算得的 $\beta_m$ 和每组的 $x_m$ 计算出的 $y_m'$ 减去 $y_m$ 的差，即一个误差）
第二步，验证回归模型的正确性（即，是不是线性回归模型）。判断标准是 $\beta_i$ 是不是全为 0。一种思想是运用 $F$ 检验。另一种思想就是计算副判定系数 $R^2$ 。
第三步，对回归系数进行假设检验、区间估计。这里需要判定的是， $\beta_i$ 中哪些是 0。
最后对回归模型进行预测，并给出区间估计。

MATLAB 工具 regress。

# 多元二项式回归

MATLAB 工具 rstool。

# 非线性回归

需要回归分析的函数同样是使用匿名函数定义。

MATLAB 工具	用途
`nlinfit`	计算回归系数
`nlparci`	计算回归系数的置信区间
`nlpredic`	计算预测值及其置信区间
`nlintool`	工具箱函数

# 灰色模型

灰色模型类似于拟合和回归分析，但是区别是灰色模型给的参考点较少，一般用于估计行业质量发展（如“已知过去十年的指标数据，求预测未来十年的指标数据”）。更详尽的分析请移步灰色模型。

# 游程检验

用于检测一个样本序列是否排列随机。算法是将序列中大于平均值的记为 1，小于平均值的记为 0，再数连续的 0 或 1 的数量，最后查表。用到了再仔细学。