在 ACM 中第一次听到网络流,但是还没认真学就被迫退 役了。(菜的真实)
第二次是在肖老师的 算法设计与分析 课程上,大概了解了网络流的思想。
本文参考《算法设计》,对网络流的研究偏向理论,会涉及到一些证明。
# 定义
# 流网络
流网络(flow network)是一种带权有向图,但是有一个源点(source)和一个汇点(sink),每个权叫做该边的容量(capacity)。如下图。

对流网络我们有三点假设:
- 没有边进入 点,没有点离开 点
- 所有结点至少在一条边上
- 所有的容量都为整数(这点很重要,是 Ford-Fulkerson 算法会结束的前提)
# 流
流是一个比较形象的概念,好比每个有向边都是一根管道,权重代表这根管道能流多少水。
但是要想用数学定义下来,还是比较麻烦。
流是一个满足以下条件的函数:
- 对于图中任意一边 ,有
- 对于图中任意一点 ,有
这里是把每一种流法定义为了不同的函数 ,用这个函数作用于每一条 即可查看这种流法里“管道” 里流经了多少水。
流的价值: 。
最大流即为最大价值的流。
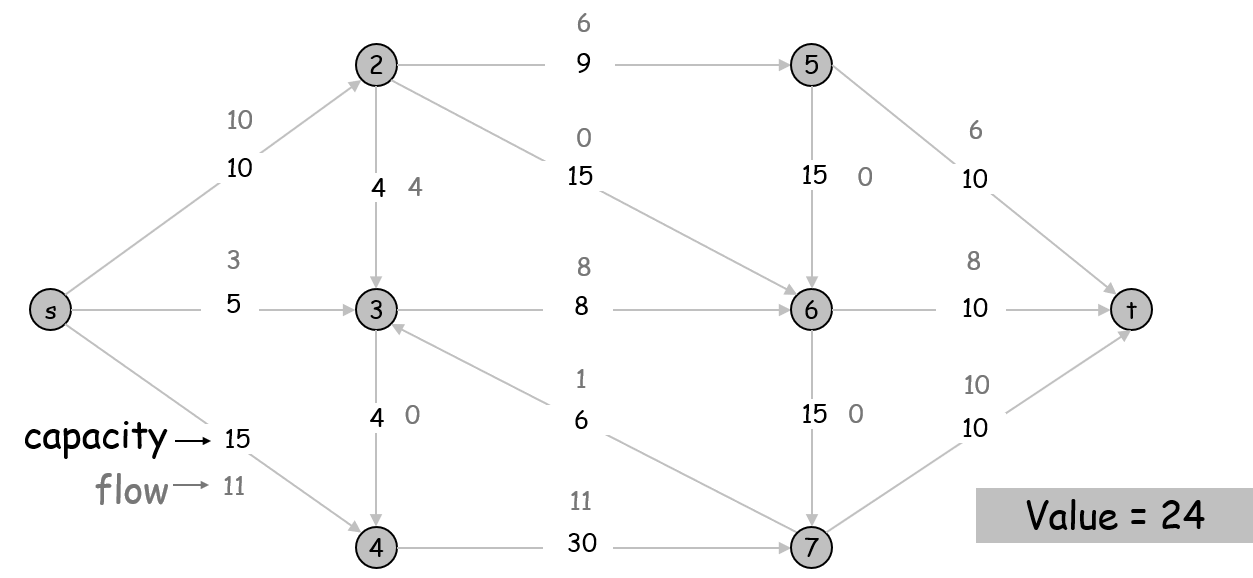
下图的一个流为 24。(但最大流为 28,从上往下流进 点的流量为 9、9、10,请读者自己思考这是如何达到的)
# 割
然后我们要引入:
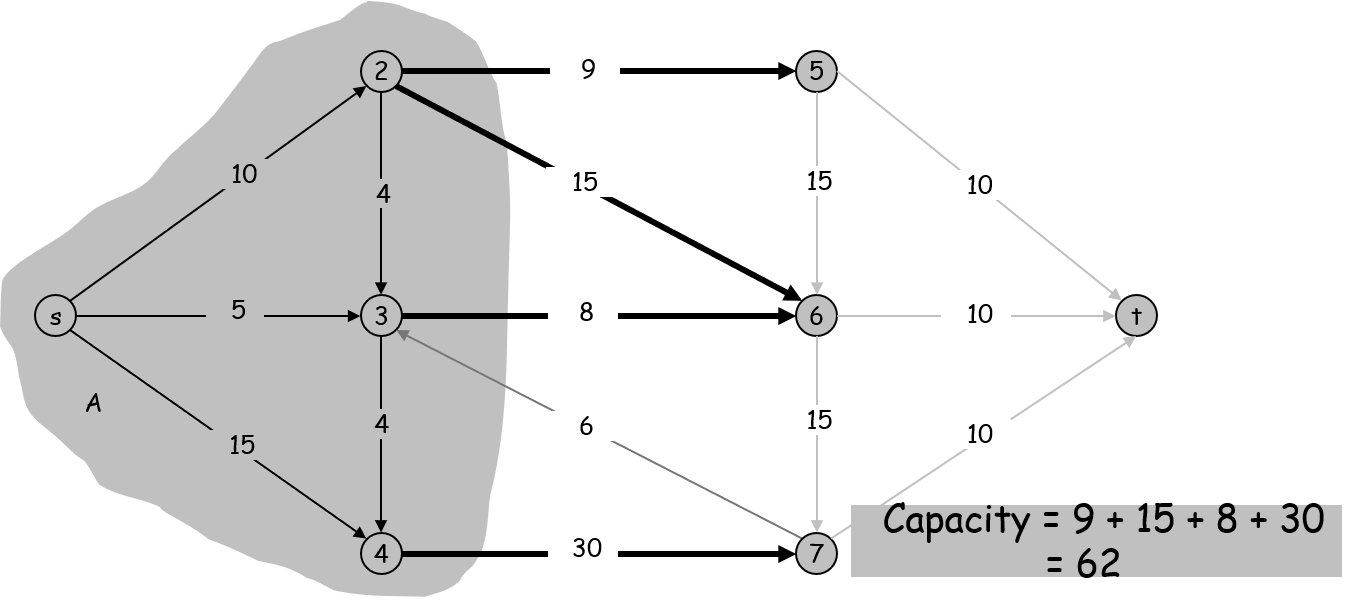
割,就是把图分为 、 两块的一种方法,要满足 块有 , 块有 。
并定义 A-B 割的容量为流出 块的所有容量之和:
最小割即指容量最小的割。
# 最大流-最小割定理
接下来我们想要证明最大流-最小割定理:
在每个流网络中,一个图中,一个 s-t 流的最大值等于一个 s-t 割的最小容量。
首先我们证明引理:
这里的 "out of" 和 "in to" 指的是穿出、穿进 块的单向边。
证明:
第三行的证明需要讨论几种情况的边:
- 如果某边 的两个点都在 内,这条边在第二行的贡献为一正一负,抵消为零;
- 如果某边 穿出了 A(即入点在 内,出点在 内),这条边在第二行的贡献为一次正值;
- 如果某边 穿入了 A(即入点在 内,出点在 内),这条边在第二行的贡献为一次负值。
综上讨论和 "out of" "in to" 的定义可得第三行的正确性。
由上面的结果,我们可以继续往下推得:对于某个图中的任意流 和任意 割,有:
证明:
那么显然地,对于一个流网络,如果找到一个流 和 ,有 ,那么 就一定是最大流,且 一定是最小割。
到这里,貌似还没有证明最大流等于最小割,因为我们不知道是不是一定存在一个流和割,满足 。
我们后面会提到 Ford-Fulkerson 算法,对于这个算法返回的流,我们可以构造一个 割使得该割等于算法返回的流,即完成了证明。
# 最大流算法
# 贪心算法
最容易想到的是先用贪心跑一下。贪心算法如下:
- 刚开始设所有边的 ;
- 找到任意一条从 连向 ,且每条边都还没有流满(即 )的路径 P。增大该路径每条边上的流;
- 反复执行上步操作直到流不动了。
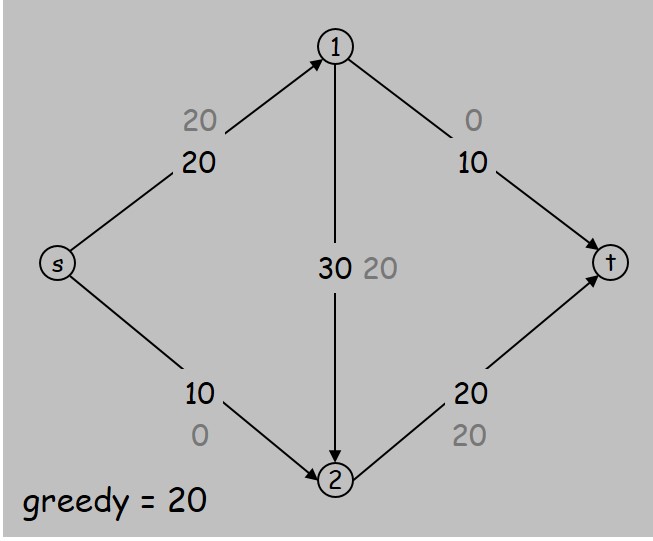
贪心在一些图上确实有很好的表现,但是很容易构造出贪心不是最优解的情况,如下:
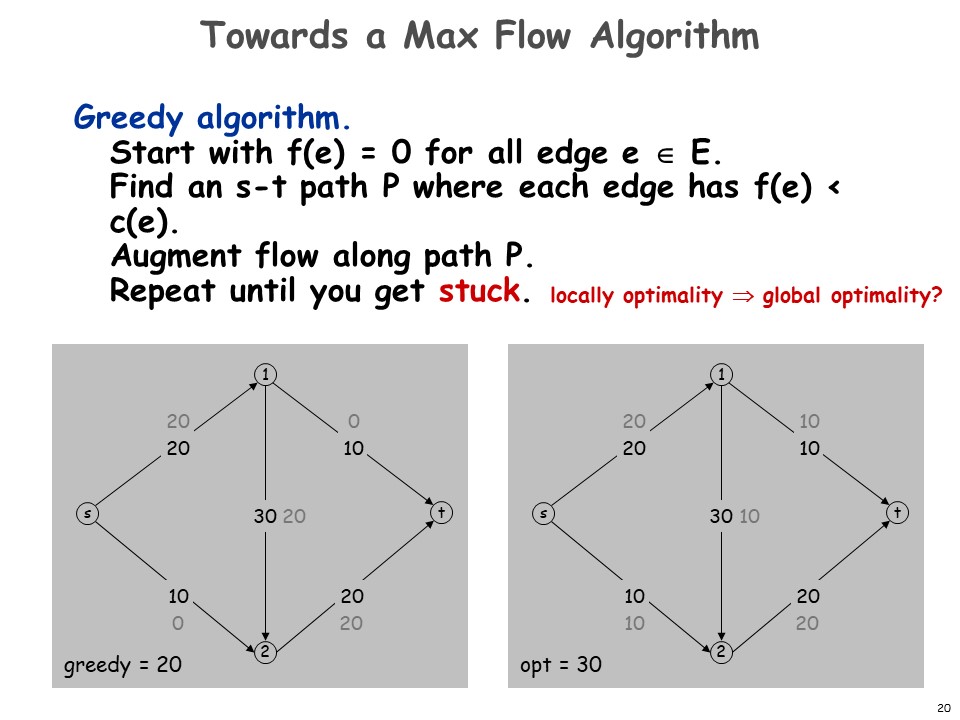
造成这个的问题是,可能会先选到一条不好的边,导致某个瓶颈满了,其他边无法继续流。
于是就想到了一种可以把已经被占满的边撤销、改回来的方法,叫剩余图(Residual graph)。
# 剩余图
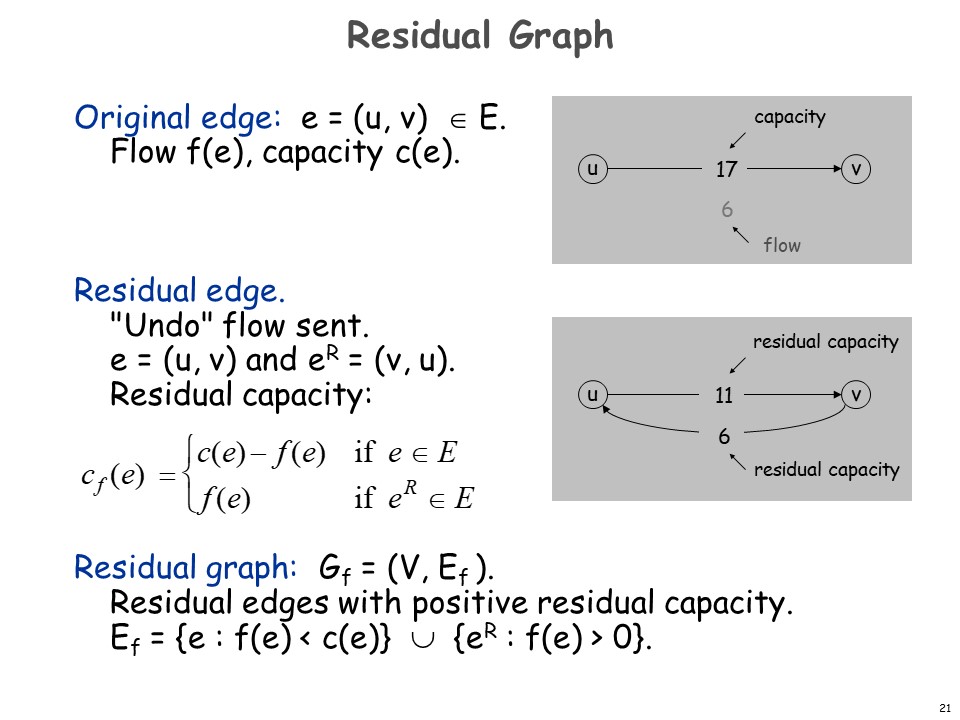
根据之前的设定,原图中的每一条边 都有 和 。
对于原图的每一条边,我们在一个新的图中都定义两条相互反向的边,把他命名叫剩余边(Residual edge)。
定义剩余边的权重(剩余容量,Residual capacity):我们把与原图的边同向的边的剩余容量设为原边还能流的量 ,把反向的边设为原边已经流过的量 。
刚才的新图便叫做剩余图(又叫残余网络,Residual graph)。
# Ford-Fulkerson 算法
良心的肖老师也提供了演示 PPT。
Ford-Fulkerson 的算法即是先建立剩余图,然后在剩余图上进行我们最开始的贪心。
在增大每边的流量时,需要减少同向边的容量,同时增加反向边的容量。
这样做的好处,就是当有一条边被正向流满,导致图中好像没有可以增加流时,此时可以使用这条边的反向边进行增加流。
如 贪心算法 提到的图中,上到下的边被流满了,如果此时开放下到上的边,就可以增加 10 的流量,即达到最大流。顺便一提,“开放一条边”这个过程被称作 “增广路”(Augmenting path)。
下面是 Ford-Fulkerson 算法的伪代码。

算法的正确性证明分为两个部分:一要证明算法会终止;二要证明算法返回的流为最大流。
算法终止的证明如下:
显然,在所有 都是整数的前提下,算法每一个步骤中的 和增广(Augment)值都一定为整数。
而每次的增广值一定大于 0,故每次增广,流的值会增长至少 1。
显然流的值不可能无限大(一个显然的上界就是 ),因此算法必然会停止。
算法返回的流为最大流的证明放在下面。
# 最大流-最小割定理证明
作个铺垫,由 Ford-Fulkerson 算法的终止条件,显然有:如果算法终止,算法返回的流不存在增广路了。
接下来我们要证明两点:一是不存在增广路的流是最大流;二是最大流等于最小割。
证明的方式是证明以下三个命题等价:
(i) 存在割 使得
(ii) 流 是最大流
(iii) 流 不存在增广路
(i) -> (ii) 由前面的引理可得。
(ii) -> (iii) 反证:如果 还存在增广路,按照 Ford-Fulkerson 的算法跑一下就可以使流的值变大,与最大流的前提矛盾。
(iii) -> (i) 设 为在最后的剩余图从源点 出发能到达的所有点的集合,。
显然 为原图的一个割,且有:
第二行的证明: 对于 out of A,一定有 ,否则:
在剩余图中仍然存在。
设 ,由 "out of" 的定义, ,。 由 的假设,在剩余图中 到 存在通路。 将该通路与 拼接,则 到 也有通路,与 矛盾。同理,对于 in to A,一定有,否则 将存在于剩余图。
证明完毕。算法的正确性也同时被证明了。
# 时间复杂度
设图中点数为 ,边的数量为 ,边的最大容量为 。
由于假设所有点都在至少一条边上,有 ,即 。
Ford-Fulkerson 算法会停止的证明中,我们证明了
- 有一个上界为 ,也就是 ;
- 算法每次迭代必定增长 1。
而每一次迭代的复杂度显然可以在 之内完成。
因此,Ford-Fulkerson 算法的时间复杂度为 。
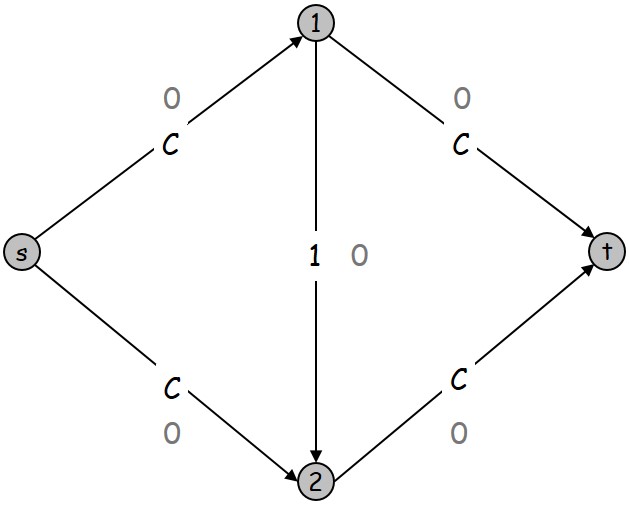
但是,这个算法不是多项式时间复杂度的!!!!这个算法是伪多项式时间复杂度的。原因是 对于输入规模是指数级的。而如果选择增广路的方法不恰当,我们构造出下图,迭代次数确实可以达到 次。
# 缩放最大流算法
问题就在于,每次选择了瓶颈(bottleneck)最小的边进行增广。能不能选择最大的边呢?于是就有了缩放最大流(Scaling Max-Flow)算法。
我们维护一个 ,迭代过程中让 由大到小。每次增广时只考虑大于 的边。下面上代码:

Dinitz、Edmonds 和 Karp 分别独立证明了增广路算法能够在
# 后记
最大流问题中还有一个经典的问题: 最小吧 费用最大流问题。请大家自学。
对于求最大流的算法, 在实践中往往使用效率更高的 Dinic 算法或 ISAP 算法(参考《算法竞赛入门经典-训练指南》)。
对于竞赛来说, 实际更重要的在于网络流模型的建立, 这时把网络流算法作为模板来使用就可以了。